Comment les fichiers 3D sont-ils générés ?

Ah ! Voilà une bonne question. Comment sont donc générés les modèles 3D publiés sur iteration3d.fr ?

build123d comme moteur principal

Sur iteration3d.fr le moteur principal de génération de fichiers 3D est basé sur l'outil build123d.

Il s'agit d'un programme python open-source de modélisation paramétrique sous Licence Apache 2.0. Ce framework repose sur le noyau géométrique Open Cascade (OCCT - maintenu par Capgemini). Le célèbre logiciel de modélisation open-source Freecad utilise ce même noyau. build123d peut être considéré comme une évolution de CadQuery.

Qu’est-ce que la modélisation paramétrique ?

Lorsqu'on utilise Fusion360 ou Sketchup on est habitué à dessiner un "sketch" à la souris ou au stylet puis à l'extruder afin d'obtenir un volume 3D. La façon de produire un volume avec la modélisation paramétrique est totalement différente. Plutôt que de "dessiner en 3D", on programme en 3D.

Openscad est un programme qui repose sur ce principe et constitue une première porte d'entrée accessible vers la modélisation paramétrique. Pour faire simple, chaque "forme" a sa déclaration. Sous Openscad l'instruction cube([10, 10, 10]) générera un cube (vous l'aurez compris) de 10x10x10. Facile, non ? Créez un autre cube, déplacez-le avec une autre instruction et petit à petit votre programme crée un nouvel objet 3D.

build123d repose sur le même principe, d'une manière plus complète et donc plus complexe, quoique. La documentation build123d propose d'ailleurs un tutoriel de transition depuis Openscad.

La puissance de Python dans build123d

La principale force de build123d est de tirer pleinement parti du puissant langage de programmation Python. Nous nous arrêterons ici, l'objectif de cette page étant pédagogique, mais les développeurs décèleront le potentiel de ce langage de codage appliqué à la modélisation paramétrique.

A titre d'exemple le code build123d suivant produira un pavé de 100 x 42 x 57 mm (Modèle #768) :

from build123d import * 

with BuildPart() as thisObject:
    Box(100, 42, 57)
            

Il existe bien entendu tout un jeu d'instructions pour déplacer, fusionner, soustraire, etc. Il est ainsi possible de produire des volumes 3D très complexes et surtout de manière paramétrique, donc facilement modifiables en agissant sur les variables que vous aurez définies.

Comment débuter avec build123d ?

Pour commencer à modéliser avec build123d, il vous faudra disposer de simples, mais nécessaires, bases en programmation Python.

Build123d propose une solide documentation.

Le meilleur point de départ est sans doute ce tutoriel simple et complet du design d'une pièce 3D avec build123d. Puis de nombreux exemples exemples sont proposés.

Build123d dispose d'un salon Discord très réactif, avec notamment des interventions des développeurs du projet.

Pour faciliter (grandement) le débogage, il est très utile d'installer l'interface graphique OCP CAD Viewer for VS Code qui s'intègre très facilement directement dans Visual Studio Code.

Vous pouvez retrouver le dépôt GitHub officiel de build123d ici.

Et pour conclure : merci build123d, merci CadQuery, merci OCCT, merci Python !

Tutoriel complet build123d

Pour ce tutoriel, nous prendrons appui sur le template Bol / Pot 3D. Comme vu plus haut, nous utilisons comme éditeur de code source Visual Studio Code, et OCP CAD Viewer for VS Code pour visualiser à l'ecran les figures et modèles produits. Les captures d'écran affichées dans ce tutoriel sont issues de OCP CAD Viewer for VS Code.

Définir les paramètres et importer les outils

Partons du principe que nous souhaitons définir notre bol avec ces paramètres :

• inner_bottom_diam pour le diamètre intérieur de la base du bol
• inner_top_diam pour le diamètre intérieur du haut du bol
• inner_height pour la hauteur intérieure du bol
• thickness pour l'entièreté de l'épaisseur de la paroi

Il s'agit là d'une étape décisive qui va déterminer toute la construction du code. Vous pouvez consulter la page Génération de fichiers 3D à la demande : le process pour en savoir plus sur cette première étape qui fait partie d'un processus global.

Nous souhaitons par ailleurs que la base du bol soit arrondie au niveau de l'angle, nous introduisons donc une nouvelle variable bend_fillet que nous fixons à 1.

Nous obtenons ainsi ces premières lignes de code :

from build123d import *
from ocp_vscode import show

from math import atan2, tan, pi

# --- Inputs ---
inner_bottom_diam = 50
inner_top_diam    = 80
inner_height      = 70
thickness         = 2

bend_fillet       = 1.0
    

D'après ces premières lignes nous souhaitons donc un bol dont la paroi sera épaisse de 2, la hauteur interne de 70, le diamètre interne bas de 50 et le diamètre interne haut de 80.

On remarque plusieurs lignes commençant par import. Ces lignes importent plusieurs librairies Python nécessaires au script :

• from build123d import * – importe toutes les fonctions de Build123d, la librairie de modélisation 3D paramétrique utilisée pour créer les formes.
• from ocp_vscode import show – importe la fonction show() de ocp_vscode, qui permet d’afficher les modèles 3D directement dans VS Code.
• from math import atan2, tan – importe des fonctions de la librairie standard math pour les calculs trigonométriques et géométriques.

Dessiner un chemin

Nous souhaitons générer un bol. Un bol est une forme symétrique autour d’un axe central : il peut être obtenu par révolution d’un profil 2D, dont la rotation crée une géométrie parfaitement régulière tout autour de cet axe. Nous allons donc dans un premier temps générer un chemin, un path, qui sera plus tard support de la révolution.

Ce chemin va être défini par trois points. Le premier est positionné à l'origine (0.0,0.0) et le second positionné le long de l'axe X, à la distance inner_bottom_diam de l'origine (inner_bottom_diam / 2.0, 0.0). On divise par deux pour obtenir le rayon à partir du diamètre.

Pour le troisème point (le haut du vase), les choses sont un peu complexes. Choix est fait que les rebords du bol soient parallèles à la base (parallèle à l'axe X), et non inclinés. Difficile à imager et à expliciter à ce stade, mais nous allons volontairement placer le troisième point deux fois plus que prévu, donc deux fois plus haut que la hauteur intérieure, inner_height. Pour pouvoir "étirer" ce segment nous allons calculer l'angle résultant des dimensions fixées pour notre bol. Puis, selon que l'angle est droit ou non, un traitement spécifique est appliqué.

Il en résulte le code suivant :

from build123d import *
from ocp_vscode import show

from math import atan2, tan

# --- Inputs ---
inner_bottom_diam = 50
inner_top_diam    = 80
inner_height      = 70
thickness         = 2


bend_fillet       = 1.0


x0, y0 = 0.0, 0.0
x1, y1 = inner_bottom_diam / 2.0, 0.0

dx0 = (inner_top_diam - inner_bottom_diam) / 2.0
dy0 = inner_height
angle_rad = atan2(dy0, dx0)

y2 = inner_height * 2.0
if abs(dx0) < 1e-9: # vertical wall case (top==bottom)
    x2 = x1
else:
    x2 = x1 + y2 / tan(angle_rad)

    

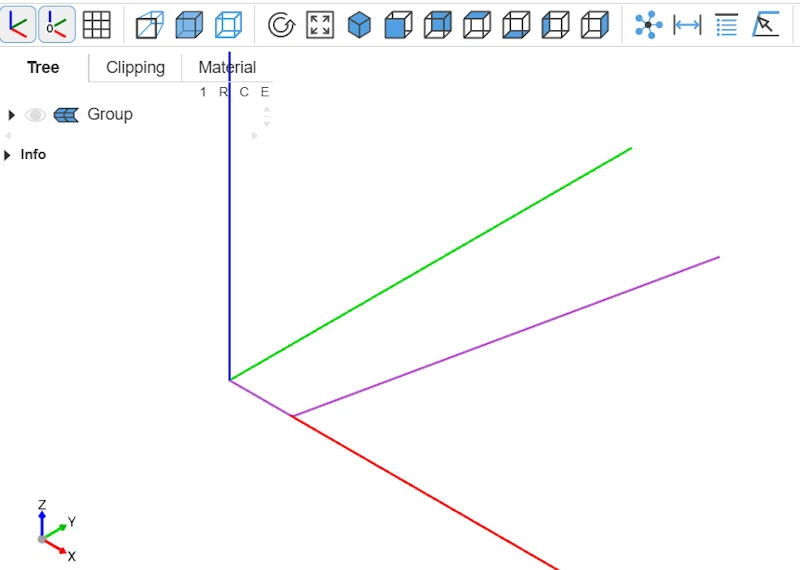
Maintenant que nous disposons des trois points, nous allons pouvoir réaliser le path. Pour ce faire nous utilisons FilletPolyline qui permet de générer un path en incluant un fillet (arrondi) afin que la base de notre bol soit adoucie. FilletPolyline est la première fonction de construction que nous utilisons dans notre script. show nous permet de visualiser le chemin, en violet à l'écran.

from build123d import *
from ocp_vscode import show

from math import atan2, tan

# --- Inputs ---
inner_bottom_diam = 50
inner_top_diam    = 80
inner_height      = 70
thickness         = 2


bend_fillet       = 1.0


x0, y0 = 0.0, 0.0
x1, y1 = inner_bottom_diam / 2.0, 0.0

dx0 = (inner_top_diam - inner_bottom_diam) / 2.0
dy0 = inner_height
angle_rad = atan2(dy0, dx0)

y2 = inner_height * 2.0
if abs(dx0) < 1e-9: # vertical wall case (top==bottom)
    x2 = x1
else:
    x2 = x1 + y2 / tan(angle_rad)

# 1) Filleted polyline (wire path)
with BuildLine() as ln:
    FilletPolyline((x0, y0), (x1, y1), (x2, y2), radius=bend_fillet)
path = ln.wire()

show(path)

            

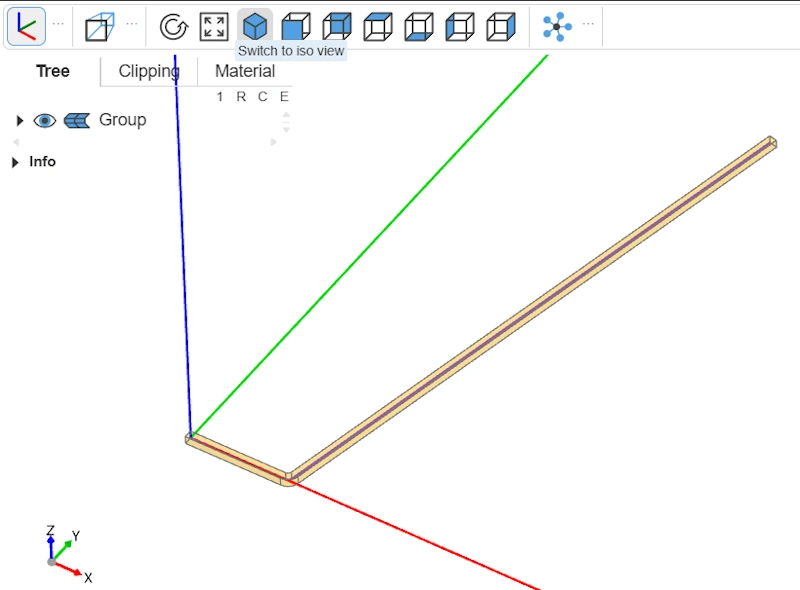
Extruder une forme 3D

Pour pouvoir réaliser la révolution autour de l'axe Y, nous avons besoin d'un profil 2D, d'une forme fermée, d'une face. Ici le path n'est qu'un segment. Nous allons donc "extruder" un carré selon ce path afin d'obtenir une sorte de barre cintrée en 3D.

Pour ce faire nous utilisons les fonctions de construction Rectangle et sweep. Rectangle permet de définir un rectangle 2D (ici un carré, la longueur du rectangle étant égal à sa largeur) de côté thickness, l'épaisseur souhaitée des parois de notre bol. sweep permet de "balayer" le profil de notre carré le long du path et ainsi créer une forme 3D, une barre cintrée ici affichée en transparence grâce à transparent=True.

from build123d import *
from ocp_vscode import show

from math import atan2, tan

# --- Inputs ---
inner_bottom_diam = 50
inner_top_diam    = 80
inner_height      = 70
thickness         = 2


bend_fillet       = 1.0


x0, y0 = 0.0, 0.0
x1, y1 = inner_bottom_diam / 2.0, 0.0

dx0 = (inner_top_diam - inner_bottom_diam) / 2.0
dy0 = inner_height
angle_rad = atan2(dy0, dx0)

y2 = inner_height * 2.0
if abs(dx0) < 1e-9: # vertical wall case (top==bottom)
    x2 = x1
else:
    x2 = x1 + y2 / tan(angle_rad)

# 1) Filleted polyline (wire path)
with BuildLine() as ln:
    FilletPolyline((x0, y0), (x1, y1), (x2, y2), radius=bend_fillet)
path = ln.wire()



# 2) Sweep a square section along that path
with BuildPart() as swept:
    with BuildSketch(path ^ 0):
        Rectangle(thickness, thickness, align=(Align.MAX, Align.MIN))
    sweep(path=path, transition=Transition.RIGHT)

show(path, swept, transparent=True)
            

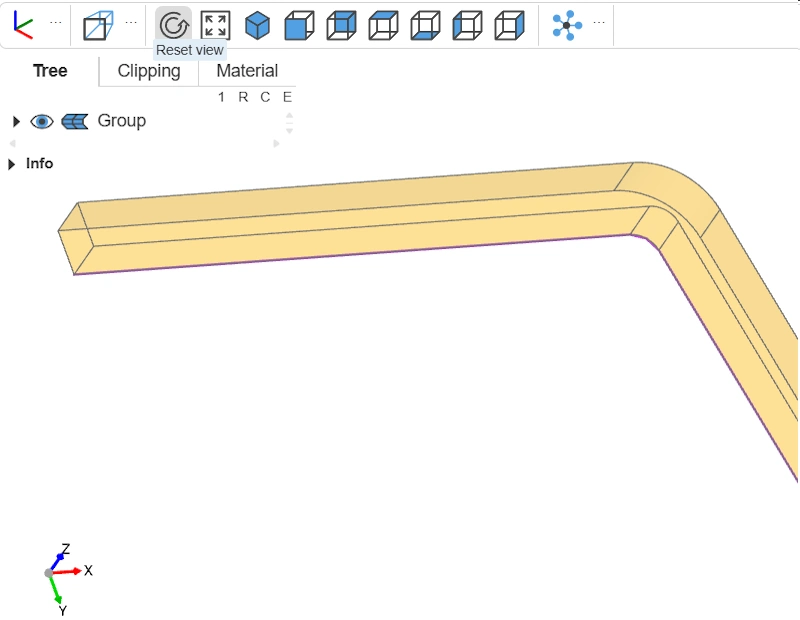
Couper la forme 3D

Pour rappel, nous avons "étiré" le bras incliné. Il convient à présent de le couper. Pour ce faire on définit la hauteur de coupe à thickness + inner_height, soit l'épaisseur + la hauteur interne. Ce sera la hauteur complète du bol.

Si l'on observe bien la forme 3D à ce stade, on remarque qu'elle n'est pas alignée le long de X mais décalée de thickness sous l'axe X. Le plus simple aurait été de déplacer la pièce vers Y+ de la valeur de thickness. Mais nous allons faire autrement afin de développer la notion de recherche de face.

Si l'on souhaite couper à thickness + inner_height il faut que l'on se positionne sous la forme 3D. Nous utilisons ici la fonction filter_by(Plane.XZ) pour sélectionner uniquement les faces parallèles au plan XZ de la pièce balayée. Ensuite, nous les trions par leur position selon l’axe Y grâce à sort_by(Axis.Y) afin d’obtenir la face la plus basse, qui servira de référence.

...

# 3) Cut the angled arm using a plane parallel to XZ
target_y = thickness + inner_height

# Pick the lowest XZ-parallel face as a reference
xz_faces = swept.part.faces().filter_by(Plane.XZ).sort_by(Axis.Y)

ref_face = xz_faces[0]  # EN: lowest-Y face

# Build a reference plane from that face
ref_plane = Plane(ref_face)

show(path,swept.part,ref_plane)

...

            

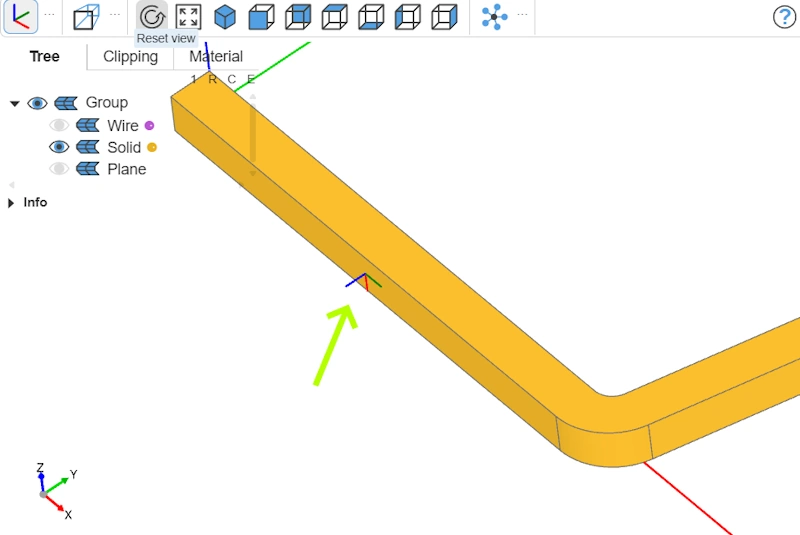
À présent, nous souhaitons nous assurer que la normale du plan de référence pointe bien vers le haut, c’est-à-dire dans la direction de l’axe +Y, comme pour le plan standard Plane.XZ. Si la normale est orientée à l’inverse (vers −Y), elle est inversée. Ensuite, nous calculons la distance de décalage entre la position actuelle du plan et la hauteur cible Y = thickness + inner_height. Cette valeur permet de créer un nouveau plan décalé (cut_plane) exactement à la bonne altitude pour effectuer la coupe. Puis nous coupons notre forme 3D avec split.

from build123d import *
from ocp_vscode import show

from math import atan2, tan

# --- Inputs ---
inner_bottom_diam = 50
inner_top_diam    = 80
inner_height      = 70
thickness         = 2


bend_fillet       = 1.0


x0, y0 = 0.0, 0.0
x1, y1 = inner_bottom_diam / 2.0, 0.0

dx0 = (inner_top_diam - inner_bottom_diam) / 2.0
dy0 = inner_height
angle_rad = atan2(dy0, dx0)

y2 = inner_height * 2.0
if abs(dx0) < 1e-9: # vertical wall case (top==bottom)
    x2 = x1
else:
    x2 = x1 + y2 / tan(angle_rad)

# 1) Filleted polyline (wire path)
with BuildLine() as ln:
    FilletPolyline((x0, y0), (x1, y1), (x2, y2), radius=bend_fillet)
path = ln.wire()



# 2) Sweep a square section along that path
with BuildPart() as swept:
    with BuildSketch(path ^ 0):
        Rectangle(thickness, thickness, align=(Align.MAX, Align.MIN))
    sweep(path=path, transition=Transition.RIGHT)



# 3) Cut the angled arm using a plane parallel to XZ
target_y = thickness + inner_height

# Pick the lowest XZ-parallel face as a reference
xz_faces = swept.part.faces().filter_by(Plane.XZ).sort_by(Axis.Y)

ref_face = xz_faces[0]  # EN: lowest-Y face

# Build a reference plane from that face
ref_plane = Plane(ref_face)

show(path,swept.part,ref_plane)

# Ensure the plane's normal points to +Y (same convention as Plane.XZ) so Keep.TOP keeps the upper side
if ref_plane.z_dir.dot(Vector(0, 1, 0)) < 0:
    ref_plane = Plane(ref_plane.origin, ref_plane.x_dir, -ref_plane.z_dir)

# Compute the signed offset to reach target Y (thickness + inner_height)
offset_dist = target_y - ref_plane.origin.Y
cut_plane = ref_plane.offset(offset_dist)



with BuildPart() as trimmed:
    add(swept.part)
    split(bisect_by=cut_plane, keep=Keep.BOTTOM)

final_part = trimmed.part

show(path,final_part)
            

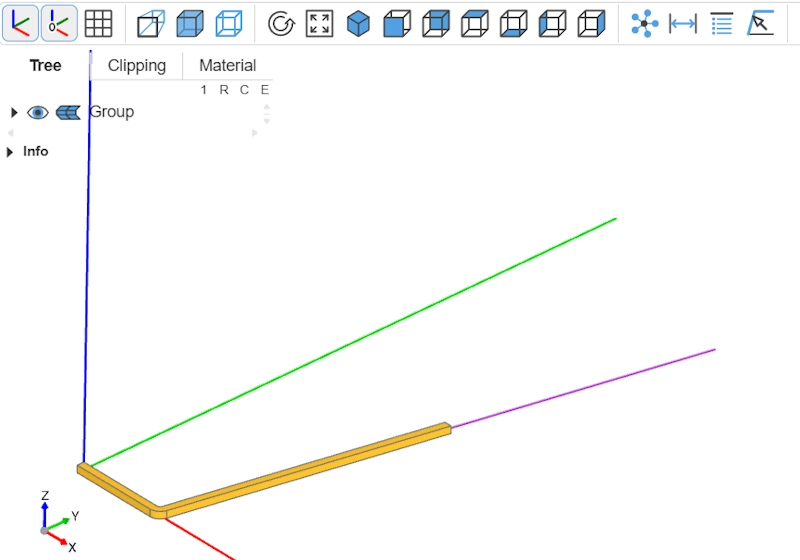
Préparer la face de révolution

Pour rappel, l'objectif de cette construction d'une barre cintrée en 3D est d'obtenir un profil à faire tourner autour de l'axe Y. Mais il n'est pas possible d'appliquer une révolution sur un solide. Aussi nous allons récupérer la face de la barre cintrée qui se trouve sur le plan XY.

...
# 4) Get the seed_face (face lying on the XY plane, i.e., Z ≈ 0)
xy_faces = final_part.faces().filter_by(Plane.XY)

# Pick the XY face whose plane is closest to Z = 0
seed_face = min(xy_faces, key=lambda f: abs(Plane(f).origin.Z))

show(path,seed_face)
...
            

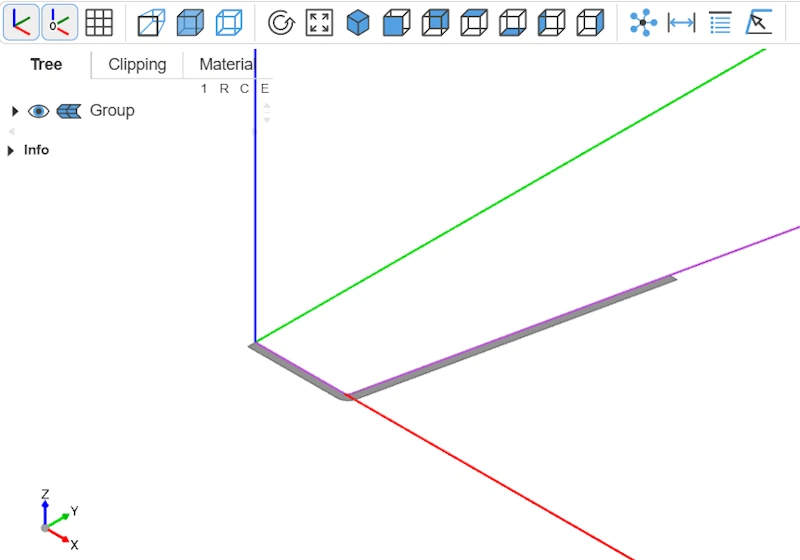
Révolution (revolve)

Nous y sommes ! Nous pouvons à présent appliquer la révolution avec revolve.

from build123d import *
from ocp_vscode import show

from math import atan2, tan

# --- Inputs ---
inner_bottom_diam = 50
inner_top_diam    = 80
inner_height      = 70
thickness         = 2


bend_fillet       = 1.0


x0, y0 = 0.0, 0.0
x1, y1 = inner_bottom_diam / 2.0, 0.0

dx0 = (inner_top_diam - inner_bottom_diam) / 2.0
dy0 = inner_height
angle_rad = atan2(dy0, dx0)

y2 = inner_height * 2.0
if abs(dx0) < 1e-9: # vertical wall case (top==bottom)
    x2 = x1
else:
    x2 = x1 + y2 / tan(angle_rad)

# 1) Filleted polyline (wire path)
with BuildLine() as ln:
    FilletPolyline((x0, y0), (x1, y1), (x2, y2), radius=bend_fillet)
path = ln.wire()



# 2) Sweep a square section along that path
with BuildPart() as swept:
    with BuildSketch(path ^ 0):
        Rectangle(thickness, thickness, align=(Align.MAX, Align.MIN))
    sweep(path=path, transition=Transition.RIGHT)



# 3) Cut the angled arm using a plane parallel to XZ
target_y = thickness + inner_height

# Pick the lowest XZ-parallel face as a reference
xz_faces = swept.part.faces().filter_by(Plane.XZ).sort_by(Axis.Y)

ref_face = xz_faces[0]  # EN: lowest-Y face

# Build a reference plane from that face
ref_plane = Plane(ref_face)

# Ensure the plane's normal points to +Y (same convention as Plane.XZ) so Keep.TOP keeps the upper side
if ref_plane.z_dir.dot(Vector(0, 1, 0)) < 0:
    ref_plane = Plane(ref_plane.origin, ref_plane.x_dir, -ref_plane.z_dir)

# Compute the signed offset to reach target Y (thickness + inner_height)
offset_dist = target_y - ref_plane.origin.Y
cut_plane = ref_plane.offset(offset_dist)



with BuildPart() as trimmed:
    add(swept.part)
    split(bisect_by=cut_plane, keep=Keep.BOTTOM)

final_part = trimmed.part


# 4) Get the seed_face (face lying on the XY plane, i.e., Z ≈ 0)
xy_faces = final_part.faces().filter_by(Plane.XY)

# Pick the XY face whose plane is closest to Z = 0
seed_face = min(xy_faces, key=lambda f: abs(Plane(f).origin.Z))


# 5) Revolve the seed_face into a solid bowl
with BuildPart() as revolved:
    revolve(seed_face, axis=Axis.Y)
final_part = revolved.part

show(path,final_part)

            

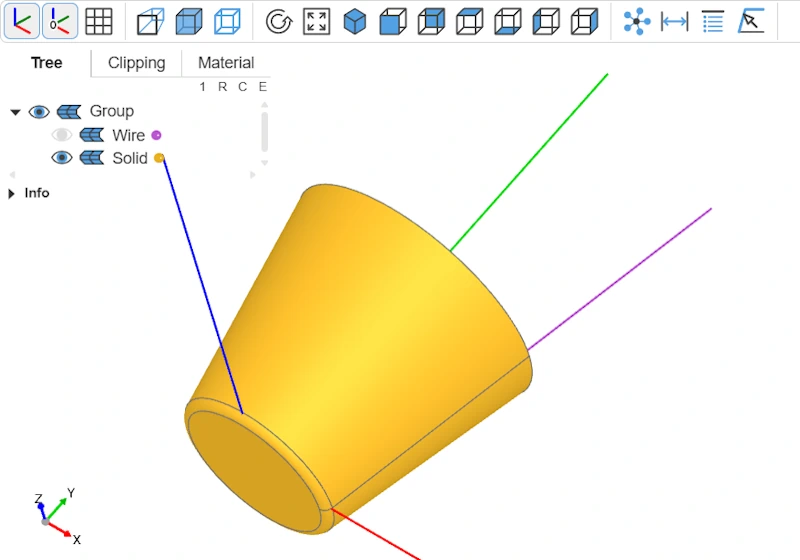
Appliquer des arrondis

Les arêtes des rebords sont pour le moment franches. Nous allons y appliquer un arrondi. Pour l'esthétique, mais surtout pour traiter cette problématique des fillets qui peut être déroutante. Un simple clic sur l'arête à arrondir comme dans Fusion360 ne suffit pas. Il va falloir aller chercher ces arêtes. Dans notre exemple, cela est assez simple. Mais cela peut s'avérer beaucoup plus fastidieux sur des modèles complexes.

Nous allons filtrer toutes les arêtes du solide pour ne conserver que celles de type circulaire (GeomType.CIRCLE), puis les trier selon leur position le long de l’axe Y afin d’isoler les deux arêtes les plus hautes, correspondant au rebord supérieur du bol.

...
# 6) Select the two highest circular edges in Y
edges_sorted = (
    final_part.edges()
    .filter_by(GeomType.CIRCLE)               # keep only circular edges
    .sort_by(Axis.Y)                          # sort by Y position
)
target_edges = edges_sorted[-2:]              # take the two highest

show(target_edges)
...
            

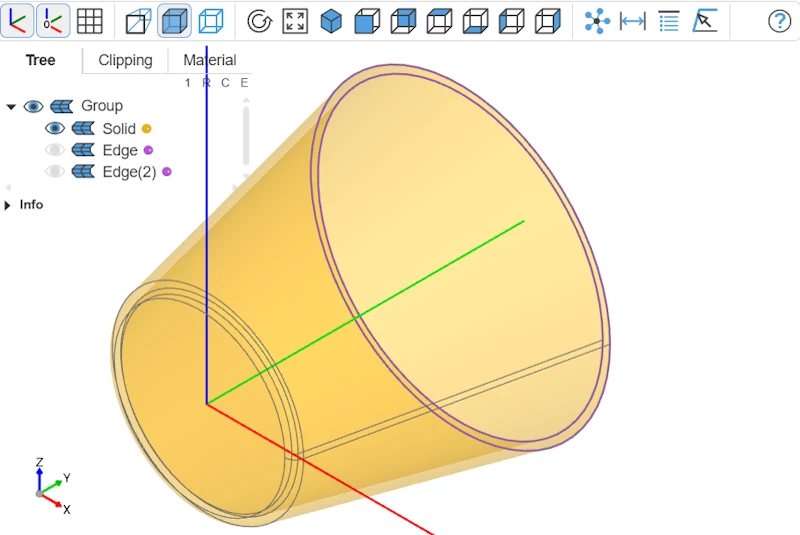
Il ne nous reste plus qu'à ajouter les arrondis avec fillet et nous obtenons le code final suivant :

from build123d import *
from ocp_vscode import show

from math import atan2, tan

# --- Inputs ---
inner_bottom_diam = 50
inner_top_diam    = 80
inner_height      = 70
thickness         = 2


bend_fillet       = 1.0


x0, y0 = 0.0, 0.0
x1, y1 = inner_bottom_diam / 2.0, 0.0

dx0 = (inner_top_diam - inner_bottom_diam) / 2.0
dy0 = inner_height
angle_rad = atan2(dy0, dx0)

y2 = inner_height * 2.0
if abs(dx0) < 1e-9: # vertical wall case (top==bottom)
    x2 = x1
else:
    x2 = x1 + y2 / tan(angle_rad)

# 1) Filleted polyline (wire path)
with BuildLine() as ln:
    FilletPolyline((x0, y0), (x1, y1), (x2, y2), radius=bend_fillet)
path = ln.wire()



# 2) Sweep a square section along that path
with BuildPart() as swept:
    with BuildSketch(path ^ 0):
        Rectangle(thickness, thickness, align=(Align.MAX, Align.MIN))
    sweep(path=path, transition=Transition.RIGHT)



# 3) Cut the angled arm using a plane parallel to XZ
target_y = thickness + inner_height

# Pick the lowest XZ-parallel face as a reference
xz_faces = swept.part.faces().filter_by(Plane.XZ).sort_by(Axis.Y)

ref_face = xz_faces[0]  # EN: lowest-Y face

# Build a reference plane from that face
ref_plane = Plane(ref_face)

# Ensure the plane's normal points to +Y (same convention as Plane.XZ) so Keep.TOP keeps the upper side
if ref_plane.z_dir.dot(Vector(0, 1, 0)) < 0:
    ref_plane = Plane(ref_plane.origin, ref_plane.x_dir, -ref_plane.z_dir)

# Compute the signed offset to reach target Y (thickness + inner_height)
offset_dist = target_y - ref_plane.origin.Y
cut_plane = ref_plane.offset(offset_dist)



with BuildPart() as trimmed:
    add(swept.part)
    split(bisect_by=cut_plane, keep=Keep.BOTTOM)

final_part = trimmed.part


# 4) Get the seed_face (face lying on the XY plane, i.e., Z ≈ 0)
xy_faces = final_part.faces().filter_by(Plane.XY)

# Pick the XY face whose plane is closest to Z = 0
seed_face = min(xy_faces, key=lambda f: abs(Plane(f).origin.Z))


# 5) Revolve the seed_face into a solid bowl
with BuildPart() as revolved:
    revolve(seed_face, axis=Axis.Y)
final_part = revolved.part


# 6) Select the two highest circular edges in Y
with BuildPart() as fp:
    add(final_part)
    edges_sorted = (
        fp.part.edges()
        .filter_by(GeomType.CIRCLE)
        .sort_by(Axis.Y)
    )
    target_edges = edges_sorted[-2:]
    fillet(target_edges, 0.6)

show(fp)
            

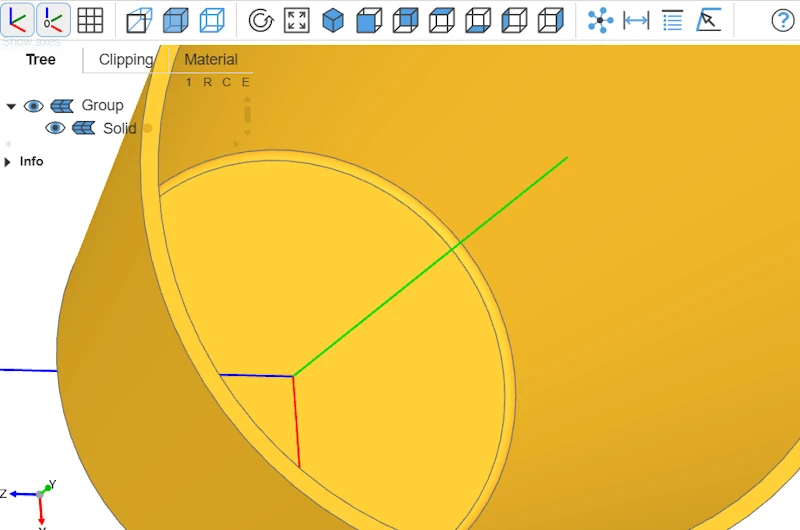
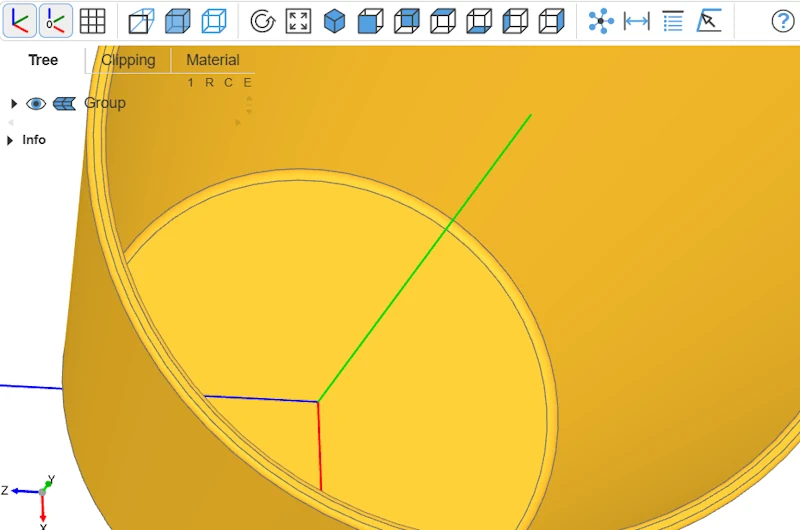
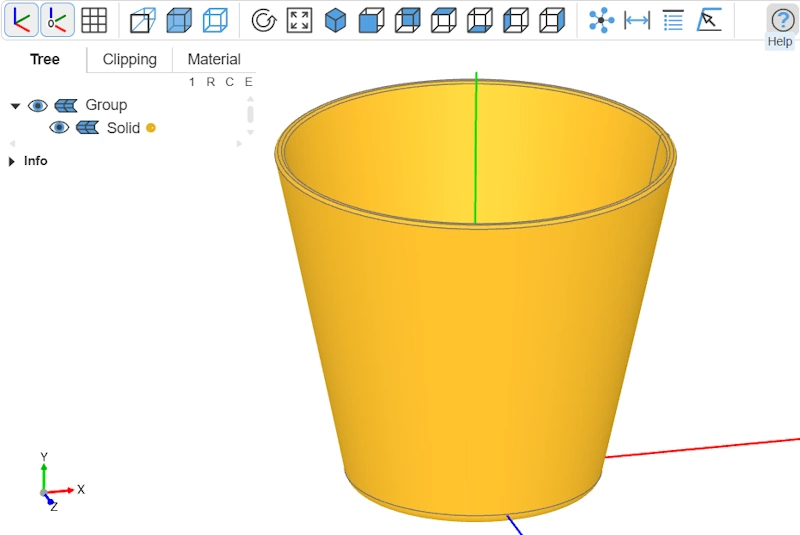
Objet final

Et voilà, notre bol est modélisé !

Comme dit en préambule ce n'est pas la façon la plus simple et la plus rapide d'obtenir ce volume 3D.

L'idée était d'explorer un maximum de fonctions de construction dans ce contexte et de donner un aperçu de la méthode de travail avec build123d. Il existe bien d'autres fonctions de construction. Et nous n'avons pas abordé ici le mode algebra.

A vous d'explorer davantage et de tirer pleinement parti de cette bibliothèse très puissante !